Decoding Circular Motion Equations

Ever wondered how a rollercoaster loops the loop without falling off the track? Or how a satellite stays in orbit? The answer lies in the fascinating world of circular motion, governed by a precise set of physics circular motion formulas. These equations unlock the secrets of objects moving in circles, revealing the forces at play and predicting their behavior. This exploration of circular motion equations aims to demystify these principles and illustrate their power in explaining everyday phenomena.
Circular motion, the movement of an object along a circular path, is a fundamental concept in physics. It differs from linear motion, where an object travels in a straight line. The key distinction lies in the continuous change in direction, even if the speed remains constant. This constant change in direction implies acceleration, which, in circular motion, is always directed towards the center of the circle, hence the term "centripetal acceleration".
The foundations of circular motion physics were laid down centuries ago by scientists like Isaac Newton. His laws of motion, particularly the second law (F=ma), provide the basis for understanding the forces involved. The realization that a force is required to maintain circular motion was a crucial step, leading to the concept of centripetal force. This force, always directed towards the center of the circle, is what keeps an object from flying off on a tangent.
Understanding physics circular motion formulas is crucial for a wide range of applications, from designing safe amusement park rides to predicting the orbits of planets. These formulas enable engineers and scientists to calculate the necessary forces, velocities, and accelerations involved in circular motion, ensuring stability and predictability in various systems. Without a deep grasp of these principles, designing functional and safe rotating machinery, satellites, or even understanding the simple motion of a spinning top would be impossible.
One of the central challenges related to circular motion formulas lies in differentiating between uniform and non-uniform circular motion. Uniform circular motion, where the speed remains constant, is governed by simpler formulas. However, non-uniform circular motion, where the speed changes, introduces additional complexities, requiring a more nuanced understanding of the underlying principles and formulas.
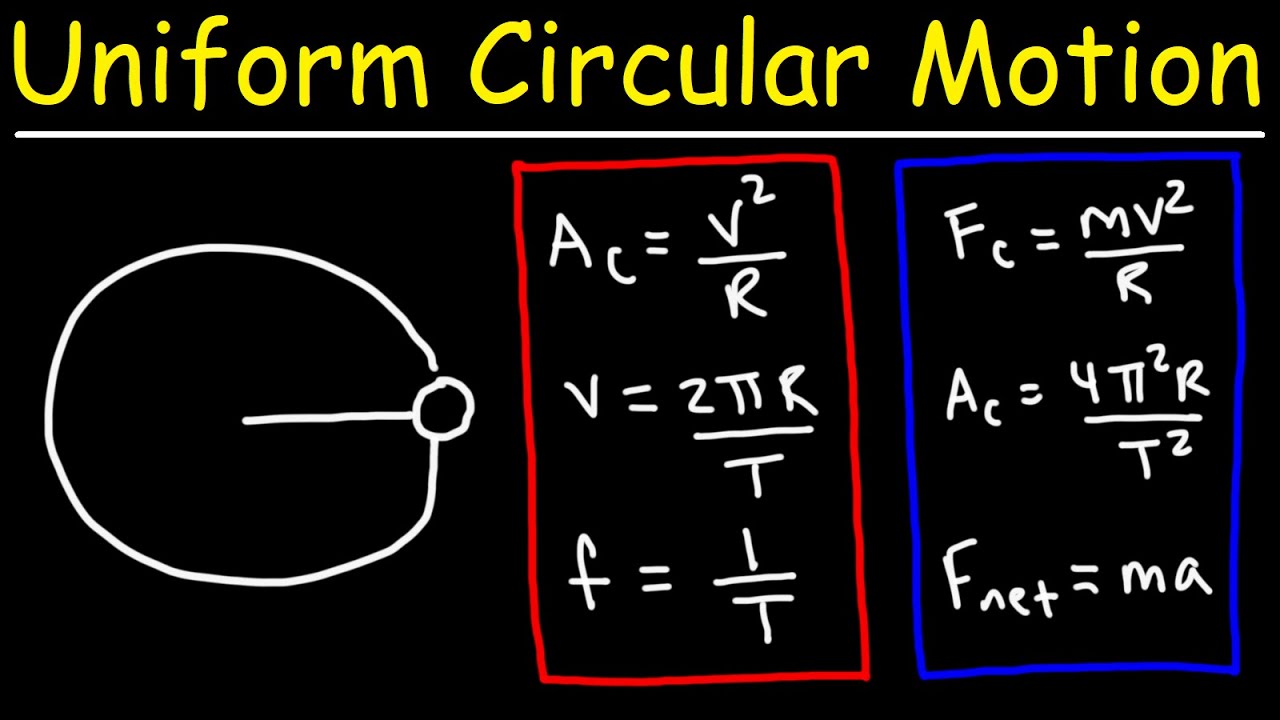
A core concept in circular motion is centripetal acceleration, defined as the rate of change of tangential velocity. It's calculated using the formula a = v²/r, where 'v' represents the speed of the object and 'r' is the radius of the circular path. Another important equation is that of centripetal force, F = mv²/r, which represents the force required to maintain circular motion.
One benefit of understanding these formulas is the ability to predict the motion of satellites. By using circular motion equations, scientists can accurately determine the orbital speed and period of a satellite. Similarly, these formulas are invaluable in designing efficient and safe curves on roads and railways, ensuring vehicles can navigate turns without skidding.
To solve circular motion problems, start by identifying the knowns and unknowns. Then, choose the appropriate formula based on the given information and the quantity you need to calculate. For example, if you know the speed and radius, you can calculate the centripetal acceleration.
Advantages and Disadvantages of Applying Circular Motion Formulas
| Advantages | Disadvantages |
|---|---|
| Predictive Power: Allows accurate prediction of object motion in circular paths. | Simplification: Basic formulas often assume ideal conditions, neglecting factors like friction. |
| Design & Engineering: Crucial for designing safe and efficient rotating machinery. | Complexity: Non-uniform circular motion introduces more complex equations. |
Five real-world examples of circular motion include a car turning a corner, a Ferris wheel, a spinning top, a satellite orbiting Earth, and an electron orbiting an atom's nucleus.
A common challenge is dealing with non-uniform circular motion, where both speed and direction change. The solution lies in applying more advanced calculus-based formulas.
Frequently asked questions include: What is centripetal force? What is the difference between speed and velocity in circular motion? What is the role of radius in circular motion? How is circular motion related to oscillations? What are some real-world examples of circular motion? How do I calculate the period of an object in circular motion? What is the difference between uniform and non-uniform circular motion? How is angular velocity related to linear velocity?
A helpful tip is to always draw a diagram of the circular motion scenario, labeling all the relevant quantities, like radius, velocity, and force.
In conclusion, understanding physics circular motion formulas is essential for grasping a wide range of phenomena, from the mundane to the extraordinary. These formulas enable us to predict and control the motion of objects in circular paths, from the design of efficient machines to the exploration of the cosmos. Mastering these principles opens a window into the fundamental workings of the universe and empowers us to harness the power of circular motion for countless applications. The continued study and application of these formulas will undoubtedly lead to further advancements in science and technology, shaping our understanding of the world around us and pushing the boundaries of human ingenuity. By recognizing the importance of these formulas, we can better appreciate the elegant simplicity and powerful predictive capabilities of physics. Delve deeper into this fascinating field and discover the intricate dance of forces and motion that governs our world.
The curious case of the locking gas cap why your car might need one
Unlocking the story behind bob joyce pictures
Unlocking the visual magic mt nebo state park photography