Découvrir l'abscisse en mathématiques
Imaginez un trésor caché sur une carte. Pour le trouver, vous avez besoin de deux informations cruciales : sa position horizontale et sa position verticale. En mathématiques, l'abscisse joue un rôle similaire, elle nous aide à localiser un point dans l'espace. Mais qu'est-ce qu'une abscisse en math exactement ?
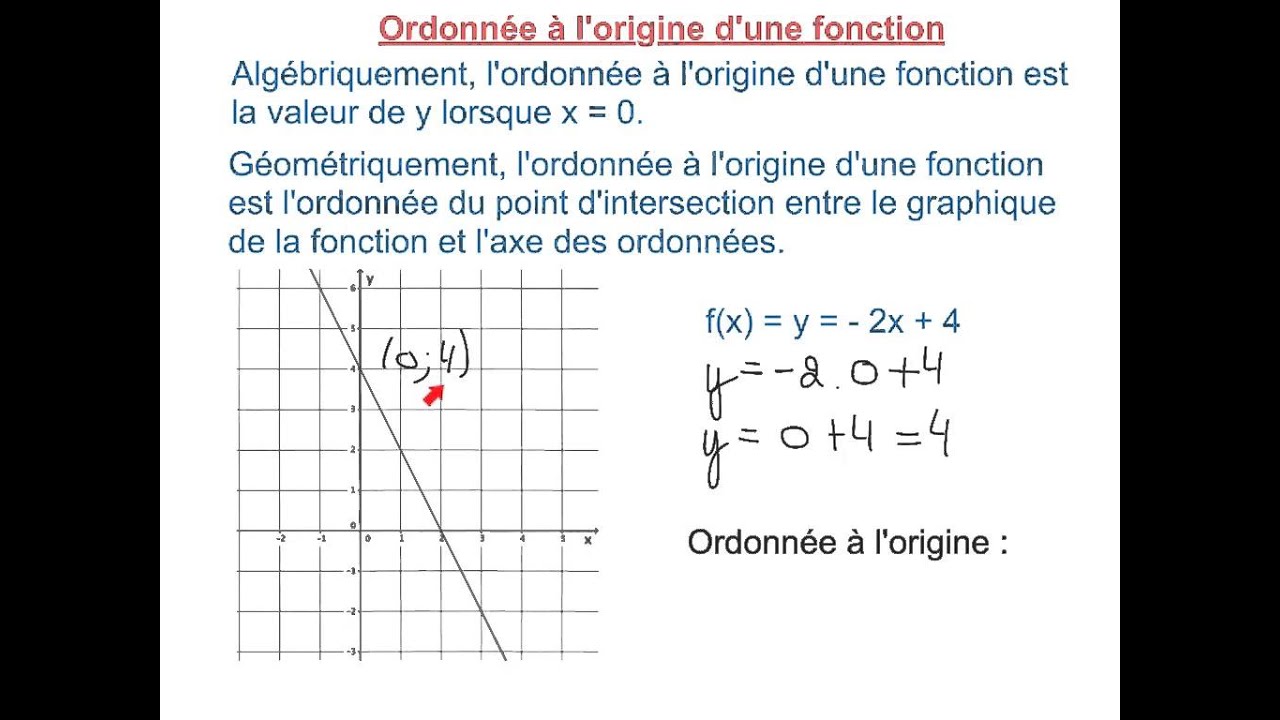
L'abscisse est la première des deux coordonnées qui définissent la position d'un point dans un plan cartésien, généralement représentée par la lettre 'x'. Elle indique la distance horizontale du point par rapport à l'axe vertical (l'axe des ordonnées). Si on visualise le plan cartésien comme une carte, l'abscisse nous dit de combien se déplacer à gauche ou à droite à partir du centre (l'origine).
Pour comprendre l'importance de la coordonnée abscisse, il faut remonter à René Descartes, le philosophe et mathématicien français qui a révolutionné la géométrie en inventant le système de coordonnées cartésiennes au XVIIe siècle. Ce système, qui porte son nom, a permis de lier l'algèbre et la géométrie, ouvrant la voie à de nouvelles découvertes en mathématiques et en physique.
Sans abscisse, il serait impossible de représenter graphiquement des fonctions, de modéliser des phénomènes physiques ou de résoudre des problèmes géométriques. De la trajectoire d'une balle de baseball à la croissance d'une population, l'abscisse est un outil essentiel pour comprendre et interpréter le monde qui nous entoure. Qu'est-ce qui se cache derrière cette notion d'abscisse et comment la maîtriser ?
Un problème courant rencontré par les débutants est la confusion entre abscisse et ordonnée. L'ordonnée, représentée par 'y', est la deuxième coordonnée d'un point et indique sa distance verticale par rapport à l'axe horizontal (l'axe des abscisses). Il est crucial de bien distinguer ces deux coordonnées pour éviter les erreurs de localisation et d'interprétation.
Prenons un exemple simple : le point (3, 2) dans un plan cartésien. L'abscisse de ce point est 3, ce qui signifie qu'il est situé à 3 unités à droite de l'origine sur l'axe horizontal. L'ordonnée est 2, indiquant une position à 2 unités au-dessus de l'origine sur l'axe vertical. La définition de l'abscisse est donc la distance horizontale qui sépare un point de l'axe vertical.
L'abscisse permet de : 1) Localiser précisément un point dans un plan, 2) Représenter graphiquement des fonctions mathématiques, 3) Modéliser des phénomènes physiques et géométriques.
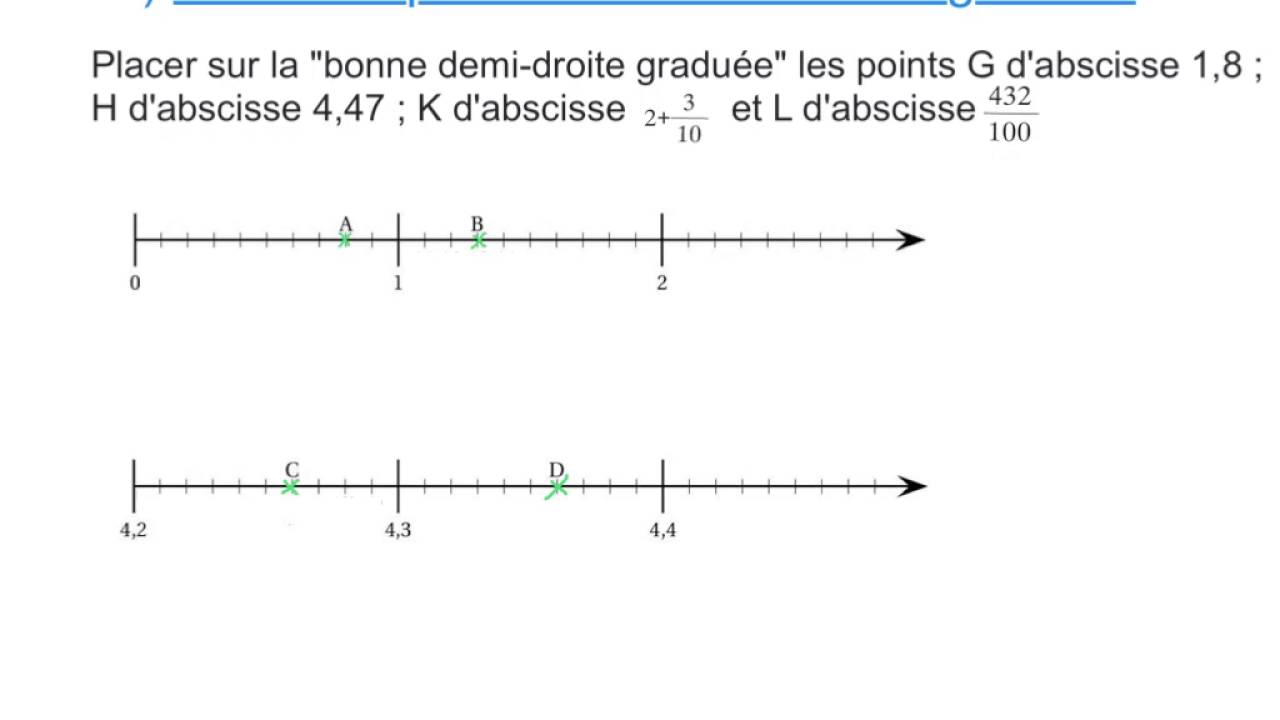
Comment utiliser l'abscisse ? Pour placer un point dans un plan cartésien, identifiez d'abord sa valeur d'abscisse sur l'axe horizontal, puis déplacez-vous verticalement selon la valeur de l'ordonnée. Exemple: pour le point (2,5), déplacez-vous de 2 unités à droite sur l'axe horizontal puis de 5 unités vers le haut.
Avantages et Inconvénients de l'utilisation de l'abscisse
| Avantages | Inconvénients |
|---|---|
| Permet la localisation précise des points | Nécessite un système de coordonnées établi |
| Facilite la représentation graphique des fonctions | Peut être difficile à visualiser en dimensions supérieures |
| Fondamentale pour la modélisation mathématique |
FAQ :
1. Qu'est-ce que l'abscisse d'un point ? Réponse : C'est sa coordonnée horizontale dans un plan cartésien.
2. Quelle lettre représente l'abscisse ? Réponse : Généralement la lettre 'x'.
3. Quelle est la différence entre abscisse et ordonnée ? Réponse : L'abscisse est la coordonnée horizontale, l'ordonnée la coordonnée verticale.
4. Comment trouver l'abscisse d'un point sur un graphique ? Réponse : En regardant sa position horizontale par rapport à l'axe vertical.
5. Qui a inventé le concept d'abscisse ? Réponse : René Descartes.
6. L'abscisse peut-elle être négative ? Réponse : Oui, si le point est à gauche de l'origine.
7. Comment utiliser l'abscisse en physique ? Réponse : Pour représenter des grandeurs physiques en fonction du temps ou d'autres variables.
8. L'abscisse est-elle toujours horizontale? Réponse: Oui, dans le système cartésien standard.
En conclusion, l'abscisse, en tant que première coordonnée d'un point dans le plan cartésien, est un concept fondamental en mathématiques. Elle permet de localiser précisément les points, de représenter graphiquement des fonctions et de modéliser des phénomènes. Comprendre l'abscisse est essentiel pour progresser en mathématiques et dans les sciences qui s'y appuient. Sa maîtrise ouvre la porte à une compréhension plus profonde du monde qui nous entoure, des trajectoires des objets à l'évolution des données. N'hésitez pas à explorer davantage les ressources en ligne et les manuels pour approfondir vos connaissances sur ce concept clé.
Trouver lobsidienne ascendante dans ark survival evolved
Plongez dans lunivers post apocalyptique avec un fond decran anime the last of us
Lelegance rustique du berger australien en normandie
